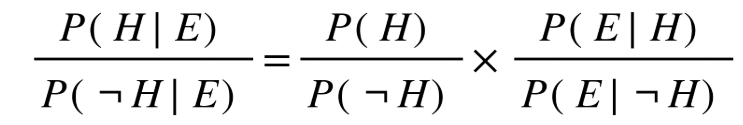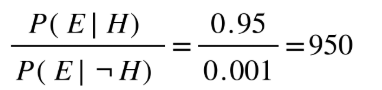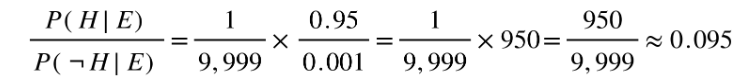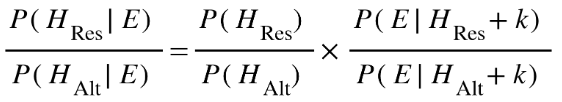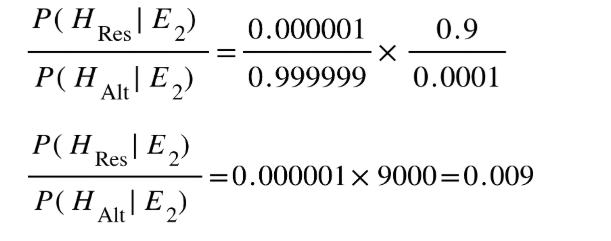Paulogia…It’s Time To Stop (Full Response)
by: Than Christopoulos / Updated: May 22, 2025 / 7:55pm EST
Editors Note- This is an academic-level version of the more pop level response I wrote.
If you want a more condensed and simpler read, please consider reading that version instead.
Summary
Paulogia, yet again, misunderstands the Max Data case for the resurrection of Jesus. This is an article unpacking the logic, and the issues with the way he and many other skeptics engage with the argument
Paulogia recently tweeted this.
This sounds clever—until you think about it for more than five seconds, because in reality, it reflects a deep misunderstanding of both the methodology and the epistemology behind historical arguments for the resurrection of Jesus. Beneath the tweet’s rhetorical smirk lies a serious confusion—one that collapses careful historical inference into the caricature of blind faith, and dismisses sophisticated evidential models by reducing them to Sunday school slogans.
Now to be clear, this kind of dismissal isn’t surprising from Paul. It’s one of his go-to rhetorical moves. Why offer detailed engagement with a nuanced model when you can say something that sounds smart—especially if you say it with confidence and derision? It’s a pattern I’ve encountered firsthand. See, for instance, how badly he misunderstood—or misrepresented—my position in his video here, and how Mike and I responded here.
So yes, I’m writing a blog post responding to a tweet. And there’s a reason for that.
I regularly get emails and messages from thoughtful people—Christians and skeptics alike—asking how to respond to one-liners like this. People feel the rhetorical weight of these kinds of objections, even when the intellectual content is hollow. That’s because tweets like Paul’s operate as intuition pumps: they bypass argument and appeal directly to audience bias. Add in a bit of well-poisoning—call your interlocutor an “Apologist” (derogatory) so your audience assumes they’re just inventing excuses—and you’ve got yourself a demagogue’s toolbox. You don’t need to make an argument. You just need to make the audience feel like one’s already been made.
The rest of this post unpacks what I think is actually going on behind Paul’s comment—philosophically, epistemically, and historically—especially in light of my past interactions with him. Because once we slow down and examine the assumptions, it becomes clear that the tweet isn’t just wrong. It reveals the very dogmatism and double standard it pretends to critique.
We’ll explore:
What the Historical Reportage Model (HRM) actually is
What the Maximal Data Case involves as a historical inference, not a theological presupposition
Why Paulogia’s objection relies on outdated and poor Humean reasoning
And how some deeper mistakes skeptic’s make when it comes to this topic.
So buckle up. While this is only going to briefly cover a lot of the important points, it is still going to be rather dense… Because once we clear away the rhetoric, what remains is just a mix of bad reasoning.
§1: The Historical Reportage Model (HRM) And The Max Data Case
Honestly, I’m a little confused that Paul is still making this mistake. In the videos I linked above, we explicitly pointed out where he collapsed categories. Apparently, saying this clearly in my debate with Matt Dillahunty wasn’t enough. Neither was the correction Mike and I offered in a livestream.
So let’s clarify what he’s trying to dismiss.
His one-liner only works if he collapses two distinct things into one. But the Historical Reportage Model (HRM) and the Maximal Data Case are two separate stages of reasoning. They are not interchangeable, and neither functions like the other.
The Historical Reportage Model (HRM)
Just like we have “models” of the universe, we can also have “models” of many other things. In this case, the HRM is a hypothesis about the genre and intent of the Gospel documents. It asks:
What kind of literature are we dealing with?
Did the authors intend to report real events in the life of Jesus as accurately as possible, based on eyewitness testimony?
That’s it.
The HRM is not a claim that the Gospels are inspired.
It is not a claim that the Gospels are inerrant.
It is not even a claim that the events described actually happened.
What the HRM affirms is this:
That the Gospel authors understood themselves to be operating within the broad genre of historical biography.
That they sought to record the deeds and teachings of Jesus in good faith, based on sources they considered reliable (including eyewitnesses and early oral tradition)
And that they did not see themselves as having literary license to invent or reshape historical events for purely theological, symbolic, or moral purposes.
To be clear…This is not question-begging—it’s a modeling assumption, used here to explore what the evidence implies if the documents are treated as testimony. For full argumentation on why the HRM is justified, see our series doing just that. If HRM holds, then the Gospels—whatever else one believes about them—function as access points to the earliest public testimony about Jesus. That includes what the original witnesses claimed happened. Again, this does not translate to
“the Gospels say X therefore X”
A critic could accept HRM and still say, “Yes, Luke wrote what he believed was accurate—but his sources were wrong.” That’s a fair counter-hypothesis. What’s not fair is pretending that HRM means “Jesus rose because the Gospels say so.” That’s either a category error—or a straw man.
In other words, HRM doesn't smuggle in the conclusion. It is only speaking on what kind of documents we are dealing with.
Why does this matter? Because the model you choose frames the data you analyze. If HRM is true, then the prior probability of a given pericope being invented is low. If a Skeptical Model is true—one where the authors felt free to fabricate or embellish—the prior probability of a given pericope being made up is high.
Again, this does not mean the events reported necessarily happened. If Luke reports that person A said X happened, and HRM holds, person A’s report of X could still be fabricated, mistaken, or embellished. The HRM simply gets us to the testimony.
So, we separate the historical investigation into two stages:
What kind of document were the Gospel authors trying to write? (HRM)
Given that, what actually happened? (Max Data Case)
The HRM answers only the first. The second depends on further evaluation. From this point forward, all of our evidential assessments assume the HRM is true. That is not question begging. It’s simply conditional reasoning: Given that the Gospels were written with serious historical intent and based on eyewitness claims, what is the probability of this evidence under competing hypotheses? If you want support for the HRM, see this series.
The Max Data Case
The Maximal Data Case builds upon the HRM but remains firmly within the domain of public historical reasoning. It asks:
If the Gospel authors were reporting eyewitness-based claims in good faith—without the freedom to invent historical details—then what best explains the content, pattern, and effects of that testimony, given the cultural, political, and religious context in which it emerged?
This is where explanatory models come in, as well as a proper methodology
The Maximal Data Case looks at historically accessible facts—such as (but not limited to):
The crucifixion of Jesus under Pontius Pilate,
The early proclamation of the resurrection in Jerusalem,
The empty tomb (as independently attested across traditions),
The poly-modal, post-mortem appearances to individuals and groups,
The conversions of skeptics like James and Paul,
And the rise of a resurrection-centric movement that exploded across hostile cultural environments…
…and it asks: “What is the probability of all this data, given the differing hypotheses and our background knowledge?”
In other words, given these data points, the question becomes: Which hypothesis best accounts for them? And this is where a formal structure is not just helpful, but necessary.
In formal terms, we are evaluating a likelihood ratio (don’t worry I will translate the math in section 3) :
Probability of the evidence given the resurrection and background knowledge
Probability of the evidence given any alternative theory and background knowledge
Where:
• E = the body of historical evidence
• HRes = the resurrection hypothesis
• HAlt = any competing hypothesis (e.g., hallucination theory, theft, legend)
• k = relevant background knowledge, including the HRM (i.e., that the Gospels are good-faith historical reportage)
Here is a simple translation of the math. The numerator (the top half) is “the probability of the evidence given the resurrection and our background knowledge” and the denominator (the bottom) is “the probability of the evidence given (any alternative hypothesis to the resurrection) and our background knowledge”
Put simply, we are just asking about the ratio of how expected the data is given any competing hypotheses. It sounds fancy, but this is just how sound reasoning works in any intellectual discipline. If some data is more expected on one hypothesis over another, then that is going to raise the probability of hypothesis.
This matters for three reasons:
HRM is part of the background knowledge (k), not the evidence.
Once granted, we treat the Gospel documents as sincere reportage—not myth, late legend, or symbolic fiction.The likelihood ratio is separate from prior probability.
Even if one assigns a low prior to the resurrection, the evidence may still be far more expected under that hypothesis than under any alternative.It gives our methodology structure.
This isn’t “what feels true.” It’s inference to the best explanation based on publicly accessible data.
Importantly, we don’t presume the resurrection. It must earn its place in the model by explaining the evidence better than all alternatives.
Of course, skeptics often appeal to low priors to dismiss the resurrection from the outset. But that’s a different discussion—one we’ll address in Section III (Humean Assumptions) and Section IV (Bayesian Priors and Background Knowledge).
For now, the point is this: the Maximal Data Case isn’t “just believe” with footnotes. It’s a rigorous, explanatory framework.
Why Skeptics Collapse The Two
Paulogia’s rhetorical move only works if he collapses two distinct stages of reasoning into one—and then flattens them into “because the Bible says so.” But why does this conflation happen so often?
There seems to be a few options on the table…one being that its just an honest mistake.
If I am being less charitable, it seems to be because if the Historical Reportage Model (HRM) is granted, the resurrection becomes too evidentially powerful to dismiss without shifting the standards. And that’s a problem for the skeptic.
Let’s be more precise.
If the Gospels are treated as sincere historical reportage based on eyewitness testimony (HRM), then we have access to the original public claims surrounding the resurrection of Jesus. That pushes the debate into the realm of inference—not theological dogma. And from there, the Maximal Data Case begins doing real explanatory work. It says: “Given this data, what hypothesis makes the most sense?”
And here’s the underlying tension: if you’re already committed to the Humean idea that miracle claims are so improbable that no amount of testimony could ever justify belief, then the Maximal Data Case becomes threatening. Because on explanatory grounds alone, the resurrection might actually come out ahead.
That puts the skeptic in an epistemically awkward position. If the data really are more probable on the resurrection hypothesis than on the alternatives, then something has to give—either the prior assumptions, or the integrity of the method.
To avoid facing that dilemma, many skeptics opt to short-circuit the conversation entirely. The move is simple: collapse the HRM and the Maximal Case into one flattened caricature—“You believe in the resurrection because the Bible says so.”
It’s rhetorically efficient. But intellectually evasive.
Not only is this both logically and mathematically mistaken (as we will see later) but it is also a move of epistemic self-protection. By conflating the two stages—literary intent and explanatory inference—the skeptic avoids having to engage either. It's much easier to mock than to methodically evaluate.
So let’s be clear:
The HRM is a claim about literary genre, authorial intention, and proximity to sources.
The Maximal Data Case is a probabilistic inference from public data to the best explanation.
Neither one assumes inspiration or inerrancy. Neither assumes the resurrection actually happened. Neither requires prior belief in a miracle. But once these distinctions are made explicit, the rhetorical power of Paulogia’s tweet dissolves.
Because now the real question is this:
If the Gospel authors were engaged in good-faith historical reportage, and the evidence is what it is—then what best explains what they claimed?
That’s where the real argument begins. And it’s precisely the argument skeptics like Paulogia prefer not to have. Let’s move on.
Hume
Paulogia’s dismissal of the Maximal Data Case as “just believe with extra steps” comes dressed with another assumption that—before even examining the data—miracle claims are disqualified on epistemic grounds. It’s Humean dogma.
And it’s one of the most persistent—and in my opinion intellectually bankrupt—moves in the modern skeptic’s playbook.
What Do Humeans Think?
In An Enquiry Concerning Human Understanding, Hume famously argued that:
“A miracle is a violation of the laws of nature; and as a firm and unalterable experience has established these laws, the proof against a miracle, from the very nature of the fact, is as entire as any argument from experience can possibly be.”
Now to be fair, there are multiple ways to interpret what Hume means here.
Some take him to be making a strong metaphysical claim: that miracles are impossible. But I don’t think Paulogia would want to endorse that stronger reading. So let’s engage with the more modest interpretation, which is more common today among philosophical skeptics.
Under the more charitable reading, Hume isn’t arguing miracles are impossible. Rather, he’s claiming they are so intrinsically improbable—so contrary to uniform human experience—that no amount of testimonial evidence could ever reasonably establish one. Why? Because testimony is always weaker than the “firm and unalterable” course of nature.
That’s the move Paulogia is making here. The Maximal Data Case could be airtight—every line of testimony could align with every independent source—and it wouldn’t matter. Because on this view, miracles are ruled out before the evidence is even considered.
Why This Isn’t Neutral Skepticism
I will offer a more in depth critique of the Humean view later on, but for now I just want to say the following. Let’s be absolutely clear: this isn’t historical caution. It’s not a call for critical thinking. It’s a built-in firewall that shields naturalism from evidential challenge by making miracle claims inadmissible by definition.
The result is a rigged game:
If you argue for a miracle based on testimony, the skeptic says testimony can never overcome the prior improbability.
If you strengthen the testimony, the skeptic insists it’s still probably fabricated or mistaken—because miracles don’t happen.
It’s an epistemic Catch-22. And notably, even non-Christian philosophers have started to move away from it.
In fact, Earman’s evaluation of Hume’s anti-miracle argument is devastating. He writes:
“When these principles [Hume’s] are made explicit and examined under the lens of Bayesianism, they are found to be either vapid, specious, or at variance with actual scientific practice.”
—John Earman, Hume’s Abject Failure, p. 70
He goes on to say that Hume maintained the illusion of a powerful argument…
“by maintaining ambiguities… and by liberal doses of sarcasm and irony”
Sounds familiar doesn’t it?
This isn’t just a weak argument—it’s bad epistemology dressed up in clever rhetoric. As Earman summarizes:
“The essay represents the kind of overreaching that gives philosophy a bad name.”
And that’s exactly the spirit of Paulogia’s tweet. It doesn’t matter what the Gospels claim, what explanatory scope the resurrection hypothesis has, or what methodological caution is employed. The conclusion is disqualified not because of the data, but because of a pre-commitment.
Why Hume (And Paulogia) are Wrong
With all this in mind…Paulogia’s objection isn’t just rhetorically dismissive—it’s also philosophically fragile. Like many modern skeptics, he borrows from a Humean framework that misunderstands probability, abuses priors, and collapses under scrutiny. In this section, we’ll show how a proper Bayesian framework undermines the entire Humean objection—and why the resurrection remains on the table as a live historical hypothesis.
What Is Bayesian Reasoning?
In order to to keep going, we need to talk about probability theory a little bit. If you want to argue that miracles are implausible, you need to speak the language of probability. That’s what David Hume tried to do—and what modern skeptics like Paulogia continue to echo. But the moment you step into that domain, you’re stepping into the world of Bayesian reasoning.
And when used correctly, Bayesian reasoning doesn’t block miracles. It simply asks us to evaluate them in proportion to the evidence.
So let’s walk through what this actually looks like.
The Basic Structure
Bayes’ Theorem gives us a formal way of updating our beliefs when we encounter new evidence. It doesn’t tell us what to believe outright—it tells us how to responsibly adjust our confidence in a hypothesis in light of new data.
The formal version looks like this, I will be using the odds form of the equation because this is going to be about competing theories.
Where..
P(H | E) = Posterior odds that the hypothesis is true, given the evidence
P(¬H | E) = Posterior odds that the alternative hypothesis is true, given the evidence
P(H) / P(¬H) = Prior odds (your initial confidence in H before seeing the evidence)
P(E | H) = Likelihood: how expected the evidence is if H is true
P(E | ¬H) = Likelihood: how expected the evidence is if H is false
What Does All This Mean?
Why use ratios in the first place?
Because we’re comparing two competing hypotheses—one that says the event or claim is true (H), and one that says it’s false (¬H). The goal isn’t to ask, “Is this absolutely certain?” but rather, “Which of these two explanations is better supported by the evidence?”
That’s exactly what the odds form of Bayes’ Theorem is built for. It gives us a way to measure how the evidence shifts the balance between two competing ideas.
What the Equation Does
Let’s break it down:
The left side of the equation tells you your final/updated odds:
How confident should I be in this hypothesis after considering the evidence?The right side is a product of two ratios:
Prior Odds — your initial confidence in H before seeing the evidence(prior probability)
Likelihood Ratio — a measure of how much more expected the evidence is if H is true versus if it’s false
The likelihood ratio is the crux of the formula. It tells us how much more expected the evidence is if one hypothesis is true compared to the alternative. And this matters—a lot. Even if your prior odds are low, you can still end up with high posterior odds if the evidence is much more expected on one side than the other.
What the Output Means
The output of the equation is an odds ratio. For example:
A result of 5:1 means that, given the evidence, the hypothesis is five times more likely than the alternative.
A result of 1:1 means the evidence doesn’t favor one side over the other.
A result of 1:10 means the hypothesis is ten times less likely than its competitor, based on the evidence.
You can also measure the output in terms of probability rather than odds. For example, take a ratio of 5/1, when done like this the output is 5. For context here, if the output is 1, the product of the prior probability and likelihood ratio is not determinate and each hypothesis is equally probable given the data and background knowledge. The closer to 0, the more likely the denominator is, and the further away from 1 trending positively (ie; from 1 to say 100, or 1000, etc.) the more likely the numerator is.
These odds can be converted to probabilities if needed, but the key idea is this: Bayes helps you weigh competing explanations in light of the evidence—and tells you which one the data leans toward. Here is the formula for converting the odds to probabilities, you’ll see me use this soon.
Here is a simple guide to understanding how odds relate to probability as well.
The Tiger Example
Imagine someone tells you they saw a tiger loose in your suburban neighborhood. You hear someone say:
“There’s a tiger loose in the neighborhood!”
Your initial reaction? No way. Tigers don’t roam the suburbs. So your prior odds—which are a way of expressing how unlikely something is before seeing new evidence—are very low. (For example, odds of 1:9,999 means a 0.01% chance.)
But now let’s break it down using Bayes' Theorem step by step:
Step 1: Define the Hypotheses
H: There is a tiger loose in the neighborhood.
¬H: There is not a tiger loose—something else is going on (a prank, misidentification, etc.)
Step 2: Assign Prior Odds
How likely did you think this was before hearing any evidence?
Let’s say:
P(H) = 1 in 10,000 → the prior probability of a loose tiger
P(¬H) = 9,999 in 10,000 → the prior probability that there isn’t
We compute the prior odds:
Step 3: Evaluate the Evidence
Now suppose:
You text 3 friends and ask them if they heard about the tiger, all of them happened to be in a group and claim to have seen the tiger themselves.
In your background knowledge, you know they are truthful people that would not play a prank on you, and you know they each have jobs in the area where the alleged tiger is loose.
That’s your (the body of evidence).
We now ask:
P(E | H): How likely is it that we’d see this evidence if there really were a tiger loose? Let’s say it’s quite high. Maybe 0.95 (95%).
P(E | ¬H): How likely is it that we’d see this same evidence if there were no tiger? Much lower. Maybe 0.001. We compute the likelihood ratio:
Step 4: Multiply by the Prior Odds
Bayes' odds form:
Now we just fill in the numbers
Step 5: Convert to Posterior Probability
We’ve been using odds so far, since Bayes’ Theorem is clearest in that form. But now we’ll convert them into probabilities so the result is easier to grasp intuitively. Remember our conversion formula is
So….
Or more simply..
Step 6: Interpret the Result
You started with near-total skepticism: just a 0.01% chance that the tiger report was true.
Then you received one compelling piece of evidence—testimony from three trusted friends who were in the right place at the right time, and who independently reported seeing the tiger.
You ran the numbers and landed at a new confidence of 8.7%.
That might still sound low. But don’t miss what just happened:
You didn’t go from “impossible” to “absolute certainty.”
You went from 1 in 10,000 to 1 in 11.5.
That’s a nearly 900-fold increase in confidence from just 3 text messages! You’re not just entertaining the idea anymore. You’re probably looking at the news, doing some google searches, texting other people, maybe even locking your door. That’s what rational belief revision looks like.
But What If More Evidence Came In?
Now imagine this:
You open your local news app—it confirms the tiger report.
There is video footage of the TIger.
Police issue a public safety alert.
Another group chat says animal control has been dispatched.
None of this is speculative. It’s concrete, independent, and mutually reinforcing. You update again.
This time, your confidence doesn’t just move to 15% or 30%.
It skyrockets to ~99%.
You’ve gone from “No way” to “I’m convinced.”
Why Spend So Much Time Explaining This?
You might be thinking: Okay, cool math. But why does this actually matter?
Because this isn’t just about tigers. Or resurrections.
It’s about how we reason—especially when the claim is surprising, uncomfortable, or unprecedented.
Bayes’ Theorem doesn’t force you to believe in miracles.
It doesn’t demand that you accept anything supernatural.
It simply formalizes one key question:
Which explanation makes the evidence more expected?
And that’s the crux.
Even if your prior confidence in a claim is extremely low, strong enough evidence can shift the scale—if that evidence is far more likely under one hypothesis than its competitors.
That’s exactly what happened in the tiger example.
You began with a skeptical prior. But when multiple pieces of independent evidence converged—school closures, news alerts, trusted witnesses, animal control—you didn’t say:
“Tigers don’t live in the suburbs, so this can’t be real.”
You let the evidence move you.
That’s the difference between reasoning and rationalizing.
One adjusts belief based on what is expected. The other blocks belief based on what is allowed.
Bayes doesn’t care how strange the claim is.
It only cares how well the claim explains what we actually see.
Let that sink in.
This Is Exactly What We’ll Do With the Resurrection
We’ll now walk through the resurrection case just like we did here—one piece of evidence at a time.
We’ll start with extreme skepticism.
We’ll examine each data point: group appearances, hostile conversions, the empty tomb, the transformation of a movement.
And we’ll let the evidence speak.
Not once will we assume the conclusion.
We’ll simply ask, at every step:
“Given this, what’s more expected—naturalism or resurrection?”
You’ll see how, even with the lowest possible prior, the explanatory power of the resurrection makes it very hard to ignore.
Let’s begin.
Applying This To The Resurrection
So far, we've seen how Bayesian reasoning helps us assess surprising claims—not by gut instinct or metaphysical veto, but by comparing how well different explanations account for the evidence.
Now, let’s plug the resurrection of Jesus into that framework. I want to be upfront about something though. In this section, I am granting a low prior probability for the resurrection for sake of simplicity. We will challenge that soon.
We start with our structure (odds form with labels for resurrection and alternative theories):
Where:
• E = the body of historical evidence
• HRes = the resurrection hypothesis
• HAlt = any competing hypothesis (e.g., hallucination theory, theft, legend)
• k = relevant background knowledge, including the HRM (i.e., that the Gospels are good-faith historical reportage)
Now the question becomes:
How much more expected is this body of evidence if Jesus really rose from the dead, versus if He didn’t?
This is our likelihood ratio—and it's the heart of the analysis.
Let’s consider just a few of the facts that I, and many other Max Data & HRM proponents argue for. As a reminder, the purpose here is not to give you the full fledged case here.
Jesus was crucified under Pontius Pilate.
His tomb was later found empty.
His followers experienced what they interpreted as post-mortem appearances of Jesus—individually, in groups, and in varying contexts.
These experiences transformed frightened followers into bold proclaimers of resurrection, even in the face of persecution and death.
These experiences were multi-sensory in nature.
This proclamation emerged in Jerusalem (the very place Jesus was buried), spread rapidly across the Roman world, and became the central claim of the earliest Christian confession.
This proclamation happened both in an anticipated hostile environment and continued to happen with voluntary suffering for no earthly reward.
and much more.
Now ask:
Would we expect all of that if Jesus stayed dead?
Would hallucinations alone explain group appearances, polymodal encounters, the empty tomb, and the explosive, resurrection-centered birth of the early church?
Would the hallucination theory predict this kind of geographical and chronological proximity between event and proclamation?
Would a conspiracy account explain the disciples’ willingness to suffer if they knew it was a lie?
The resurrection hypothesis isn’t just “one more possibility.”
It renders the totality of this evidence far more expected than any alternative.
And here’s the crucial point:
Even if you assign a skeptical prior to the resurrection, a high likelihood ratio still increases its posterior probability.
Just like the tiger in the neighborhood: your initial skepticism is real. But as the evidence rolls in—video, school closures, news alerts—you update.
Bayes doesn’t ask if you like the idea. It asks if the evidence fits.
And in the case of Jesus’ resurrection, the fit is striking.
That doesn’t mean the resurrection is proven with 100% certainty. Historical claims rarely are.
But it does mean this: If you're reasoning honestly, you can’t dismiss the resurrection by fiat.
You have to engage the data.
And if the resurrection hypothesis makes that data more probable than any alternative, it earns its place at the table—not as dogma, but as the best explanation available.
Running The Numbers
Just like our tiger example above, lets run through the topic of the resurrection with the formula. We’ve laid out the logic of Bayesian reasoning, shown how priors and likelihoods interact, and demonstrated how even unlikely hypotheses can become probable if the evidence is strong enough.
Now let’s apply that same structure to the resurrection of Jesus.
But as a reminder of two things:
First, we’re going to grant the skeptic a low prior up front. We’ll assume the lowest plausible prior imaginable—1 in a million. Why? Because if the resurrection can survive that, it can survive anything.
Second, the HRM is part of our background knowledge in this Bayesian framework—not the conclusion we’re trying to reach. It’s what allows us to assign likelihoods to what the documents say. We're asking: Given that the Gospels and Acts report claims sincerely made by early individuals, how likely is it that those individuals encountered a risen Jesus, versus being deceived, hallucinating, or lying?
Let’s walk through it, step by step—just like we did with the tiger
Define the Hypotheses
HRes = the resurrection hypothesis
HAlt = any competing hypothesis (e.g., hallucination theory, theft, legend)
Set the Initial Prior
We’ll grant:
P(HRes) = 0.000001
P(HAlt) = 0.999999
Now calculate the prior odds:
To clarify: We’re not starting with the assumption that the resurrection is likely. We’re assuming it’s extremely improbable and seeing if the evidence can still move the needle.
Sequential Evidential Updates
Now we’ll begin walking through the historical evidence—step by step—updating our probabilities as we go.
Each piece of data has already been defended in detail elsewhere (by myself and others), so we won’t re-argue every point here. Instead, the goal is to demonstrate how cumulative evidence functions within the Bayesian framework.
This is where the strength of the Historical Reportage Model—and the Maximal Data Approach—becomes clear.
Even starting from radical skepticism, the evidence doesn’t just nudge belief in the resurrection. It dramatically shifts the odds in its favor.
Lets begin!
Evidence 1: Jesus’ Crucifixion under Pontius Pilate
Virtually all scholars—across theological and skeptical lines—agree that Jesus was crucified under Pontius Pilate. This is highly expected under both P(HRes) and P(HAlt) so it does not shift our odds…but we’ll still plug it in for practice.
As a reminder, this is the odds form of Bayes.
Step 1: Assign Prior Odds
Then we calculate:
Step 2: Evaluate the Evidence and Compute the Likelihood Ratio
The evidence was equally as likely so…
Then we calculate:
Step 3: Multiply by the Prior Odds
Start with the full structure:
Now insert the numbers:
Step 4: Convert to Posterior Probability
Step 5: Interpret the Result
We started with radical skepticism: just a 1 in 1,000,000 chance that Jesus rose from the dead.
Then we evaluated the first data point — Jesus’ crucifixion under Pontius Pilate.
It didn’t move the probability. Why?
Because this event is highly expected on both hypotheses. The data is again equally probable on both the resurrection and any skeptical alternative hypothesis. I only inserted this so we can practice. The next piece of evidence is not neutral at all however.
Evidence 2: Multi-Modal Post-Mortem Appearances (to 21 Individuals)
This is where the Bayesian scales start to tip.
Following Jesus’ death, multiple groups and individuals — totaling at least 21 distinct reports found across the Gospels and Acts — are described as having seen, heard, and physically interacted with the risen Jesus. These are not vague references to dreams or isolated inner impressions. They involve multi-modal, multi-sensory encounters over a forty-day window, often in collective settings with multiple participants.
Now, crucially:
This is not an argument that “the Bible says it, therefore it happened.” That would be circular.
Rather, we are granting the Historical Reportage Model (HRM) — the view that the Gospel and Acts authors intended to report sincere, eyewitness-rooted historical testimony. We’re taking these appearance claims as what people actually said happened, and asking how expected those reports are under each hypothesis.
So: Given that these accounts most likely reflect sincere testimony from individuals who believed they encountered the risen Jesus — how likely is this body of testimony under Hₐₗₜ, compared to Hᵣₑₛ?
Let’s run the numbers and see how this evidence affects our confidence.
Step 1: Assign Prior Odds
We continue from our updated posterior odds from E₁ but remember, our priors have not changed because E1 was non-probative. So…
Now calculate the prior odds:
Step 2: Evaluate the Evidence and Compute the Likelihood Ratio
We now assess how expected this testimony is under each hypothesis.
We’ll say 0.9. This is very expected if Jesus rose bodily and appeared to His followers. Very briefly this is what we would expect to see given the resurrection.
How likely is it that this same evidence would arise under an alternative hypothesis (e.g., hallucinations, lies, metaphors)?
Much lower. Let’s say 0.0001, given that multi-modal group hallucinations are not known to occur, and coordinated falsehoods or symbolic reinterpretations this early face severe explanatory problems.
So we calculate the likelihood ratio:
Step 3: Multiply by the Prior Odds
Start with Bayes’ odds form:
Insert the numbers:
Step 4: Convert to Posterior Probability
Step 5: Interpret the Result
We’ve just made a substantial update.
You began at a 0.0001% prior, and now — after just this one line of evidence — you’re already at ~0.893%.
That might still sound low. But don’t miss the significance:
You didn’t go from “impossible” to “certain.”
You went from 1 in 1,000,000 odds to about 1 in 111 odds.
That’s a 9,000-fold increase in favor of the resurrection, from just a single evidential update.
This is what exponential growth looks like in Bayesian reasoning.
Evidence 3: Conversion of Skeptics (James and Paul)
While we could go through this a lot more, for sake of brevity, this will be the last update we do.
Two key figures—James and Paul—converted from skepticism and opposition to belief in the resurrection. These are extremely unlikely conversions on the hypothesis that Jesus stayed dead, but they are quite expected on the resurrection hypothesis, especially under the HRM.
Let’s walk through the Bayesian update:
Step 1: Assign Prior Odds
Based on our update in E2
Now calculate the prior odds:
Step 2: Evaluate the Evidence and Compute the Likelihood Ratio
We ask how expected this evidence is under each hypothesis:
Again very briefly, this is what you would expect to see if Jesus rose from the dead, but not on any of the skeptical scenarios with the HRM in the background.
Then we calculate the likelihood ratio:
This approximates how much more expected polymodal group appearances are under a resurrection model than under any known hallucination model—none of which explain visual, tactile, conversational encounters across days.
Step 3: Multiply by the Prior Odds
Start with the full structure:
Plug in the numbers…
Step 4: Convert to Posterior Probability
Step 5: Interpret the Result
You began this step with just under 1% confidence. Now you’re at nearly 88%.
That’s a radical update — and it happened because this evidence is far more expected if Jesus rose from the dead than if He didn’t.
The cumulative structure is doing its job: one piece of strong, unexpected evidence transforms the rational outlook.
But What If You’re Still Not Convinced?
Now, maybe you’ve followed the math. Maybe you’ve seen how, piece by piece, the evidential weight stacks up in favor of the resurrection. But something still feels… off.
You’re looking at the posterior probabilities, and your reaction is:
“No way. That can’t be right.”
If that’s you, I have a sneaking suspicion that one of three things is going on:
1) You Have Serious Qualms With the Evidential Assessments
And that’s fair.
If you’re thinking, “There’s no way the empty tomb has a Bayes factor of 100,” or “Skeptical conversions aren’t that rare,” then I completely understand.
A full defense of each evidential assignment is outside the scope of this blog. But I welcome that conversation, and there has been published extensive material elsewhere arguing for each estimate. For now, the point of this post is to show how the logic works once you adopt a framework like the Historical Reportage Model (HRM), not to re-argue the entire evidential basis from scratch.
If you want to dig into that, I will cover this in a future article if people want that.
2) You’re Actually Disputing the Priors — Not the Evidence
This is also common.
You might think you’re reacting to the data. But deep down, what’s really bothering you is the idea of a miracle happening at all. That’s a prior issue, not a likelihood one.
In other words:
You’re uncomfortable with the conclusion, so you’re attacking the evidence — when in reality, the disagreement lives at the level of prior probability.
This is important to recognize. Because as we’ll soon explore, many skeptics (often unknowingly) assume prior probabilities that stack the deck against any miracle, no matter the evidence.
3) You’re Judging the Data From a Different Model Than the One Being Argued
This one’s subtle, but crucial.
You might be thinking, “The Gospels are legendary. They’re theological propaganda. Why should I trust these testimonies at all?”
And if you’re assuming that model, then of course the numbers I used sound inflated. But here’s the thing:
That’s not the model this argument is working from.
This post assumes the Historical Reportage Model (HRM) — the idea that the Gospels and Acts were written as sincere, eyewitness-based historical accounts. You don’t have to agree with that model. But if you want to critique the logic of the Maximal Data Case, then you have to engage it on its own terms.
That’s not question begging. That’s just staying clear about the conditional framework we’re reasoning within.
“If the Gospels are sincere historical reportage, then how well does the resurrection hypothesis explain the data?”
That’s the question this article is answering.
If you want to challenge the HRM itself — and argue instead for a legendary-development model or a redacted-symbolic framework — we’re happy to have that discussion. But that’s a different argument than the one we’re making here.
Fine, But What About Those Low Priors?
At this point, someone might be willing to concede:
"Okay, assuming your evidential assessments are fair, you’ve shown that the resurrection hypothesis gains significant ground."
But they still object:
"Isn’t the prior probability of a resurrection just too low for any evidence to overcome?"
That’s a fair question—and a familiar one.
We previously mentioned the Humean style thoughts Paulogia has and now its time to cover those. This concern is often rooted in Humean-style objections to miracles, where the assumption isn’t that the evidence is poor, but that miracles are so unlikely a priori that they can never be reasonably believed.
Let’s walk through why this is mistaken.
The Humean Arguments For The Low Prior And How They Fail
As a reminder- This view goes back to David Hume, who famously claimed:
“A miracle is a violation of the laws of nature; and as a firm and unalterable experience has established these laws, the proof against a miracle, from the very nature of the fact, is as entire as any argument from experience can possibly be.”
In short, Hume argues that our consistent experience of the laws of nature is itself proof that a miracle didn’t occur.
The reasoning seems intuitive:
“Dead men stay dead.”
But Hume’s argument collapses under scrutiny—both philosophically and probabilistically.
1: What Are Laws of Nature?
Laws of Nature are not metaphysical forces or iron constraints.
They are regularities:
Descriptions of how nature behaves when left to itself.
But miracles—by definition—are not cases of nature left to itself. They are intentional interventions by an agent beyond nature.
So when Humeans treat the uniformity of nature as a defeater for miracles, they’re ignoring the core idea:
Miracles presuppose regularity in order to stand out.
If nature wasn’t uniform—if corpses sometimes randomly got up and walked around—then the resurrection wouldn’t be a sign of anything. It would just be weird biology.
2: The Uniformity Objection Fails Mathematically
Let’s get technical.
Let M = a miracle
Let U = the uniformity of nature (dead men stay dead, etc.)
Now suppose you say:
“Uniformity of nature makes miracles improbable.”
The Humean is asserting then…
But this violates Bayesian reasoning. Because even if P(U) is very high, it doesn’t follow that P(M | U) is low.
However, once we analyze things properly, we find that…
If P(M|U) = 1, then P(M|U) ≥ P(M)
OR if P(U|M) ≈ 1, then at worst P(M|U) ≈ P(M)
In plain English:
The existence of a regular backdrop doesn’t lower the probability of a miracle—it enables it.
The fact that our ordinary experience tells us dead men stay dead cannot be a significant piece of evidence against a resurrection because miracles could not function as a sign without the backdrop of stable natural order.
3: The Testimony Argument Also Fails
Sometimes skeptics double down:
“No amount of testimony could ever be enough to justify belief in a miracle.”
Paulogia has said this countless times. But that too fails under formal scrutiny. Consider the following result, adapted from standard Bayesian updating:
M = the hypothesis that the miracle occurred
~M = the hypothesis that the miracle did not occur
T₁...Tₙ = independent testimonies for a miracle
K = the prior odds against the miracle (can be arbitrarily low)
Then the posterior odds become:
Yes this is even more math. But it is important. Let me explain what this math means. This equation expresses a powerful result in Bayesian inference: how cumulative testimony can overturn even the most extreme initial doubt. Let’s walk through it step by step.
On the left side, we have a posterior odds ratio: This represents the odds that the miracle M occurred, versus that it didn’t (~M), after receiving a body of testimony T₁ through Tₙ. These testimonies are assumed to be independent reports, such as eyewitnesses saying they saw something miraculous.
On the right side, we break down how this result is computed using Bayesian updating.
The term 1/k represents the initial odds against the miracle—i.e., how improbable we thought the miracle was before hearing any testimonies. The smaller this is, the more skeptical our starting point.
The product term that comes after which is:
is a cumulative likelihood ratio. For each testimony Tᵢ, we compare how likely it is if the miracle really happened versus if it didn’t. If the ratio is greater than 1, that piece of testimony favors the miracle. If each testimony individually favors the miracle (even slightly), then the product grows exponentially as more testimonies are added.
Bottom line: Even if we start with very low confidence in a miracle (i.e., a large k), as long as we have enough honest, independent testimonies, and each one is more likely if the miracle happened than if it didn’t, then the overall odds in favor of the miracle can eventually become overwhelming. This is a formal, mathematical refutation of the claim that “no amount of testimony could ever justify belief in a miracle.” Testimony, when weighted properly, absolutely can.
So as long as each testimony is more expected if the miracle occurred than if it didn’t — that is,
— then the overall odds will grow exponentially.
And if we let n→∞n, you eventually get:
Okay I can feel people’s eyes rolling over so let me translate this.
What the Math Means
This result tells us something very important:
A sufficient number of independent testimonies, each with even a small evidential force, can overwhelm any finite prior against a miracle.
This destroys Hume’s “everlasting check.” A cumulative case can make any miracle credible in principle. It’s not about certainty. It’s about probabilistic momentum. And if the resurrection enjoys testimony like this, then even low priors can eventually be defeated by the weight of the evidence.
In short:
Yes, testimony can overcome low priors
No, there’s no mathematical cap on how much evidence can update your beliefs
And yes, if you deny this, you’re denying the entire structure of probabilistic inference
The “Dead Men Stay Dead” Argument—And Why It Fails
Among the many arguments skeptics use to support an exceedingly low prior probability of the resurrection, one of the most common is what we might call naive enumerative induction. It sounds technical, but it’s really just the old slogan: “Dead men stay dead”—with a statistical twist.
The objection goes like this:
“Look, this is all nice and thoughtful, but at the end of the day, the probability that someone rose from the dead is still astronomically low. Out of all the people who’ve died, how many have come back? None. That makes the statistical frequency—and thus the prior probability—effectively zero. No amount of testimony could possibly overcome that.”
Put simply, this is the “dead men stay dead” argument with a statistical spin! The statistical frequency of observed resurrections is 0. So the prior probability of the resurrection is either 0 or at least astronomically low!
At first glance this may seem like a rather intuitively true argument, but let’s unpack the logic and see how it actually leads to counter-intuitive results.
First let’s translate this into probability language.
Given a sample size of 1,000 (or any number you want) people and none have risen from the dead, the prior probability that Jesus rose from the dead is low.
Let..
k= background knowledge (sample size)
R = resurrection
P( R | k) = ~0
Here are a few reasons why this falls short
Problem 1
Look at the logic of the argument again.
The Claim: Given a sample size of 1,000 people and none have risen from the dead, the prior probability that Jesus rose from the dead is low.
So… P( Resurrection | k) = ~0
What’s wrong with this? this logic only works if we use a frequentist interpretation of probability. Frequentism says:
“The probability of A in a class B is the relative frequency of A occurring in B.”
In other words
Jesus is a human, therefore He is part of the reference class called Humans
No occurrences of humans raising from the dead in the reference class have been observed
Therefore, the probability that Jesus rose from the dead is very low
Now there are a few issues with this.
Frequentism is not the only interpretation of probability theory
There are very good reasons to not be a frequentist
If you’re asking what other interpretation there is, well, we have been using it. The Bayesian interpretation! So why prefer Bayes over Frequentism? Let me introduce you to one reason.
The Reference Class Problem
The reference class problem is the first thing that should make you doubtful of this sort of reasoning as it relates to the resurrection. Here is the basic idea.
If we assign probabilities only by looking at the occurrences of any event in a specific reference class, what happens when we attempt to add more details into our reference class? Let’s walk through an example.
What is the prior probability of me getting cancer?
Say we try to answer that question by taking a sample size of 10,000 humans and found that 300 had cancer. That means the prior probability of me getting cancer is 0.03. But there are MANY more things that inform about your risk for cancer than just being human. So we need to nuance our reference class.
Instead of just humans, what about human males? What if we changed that to human males who are Greek? What about human males that are Greek and have a family history of cancer? Okay what about human males that are Greek and have a family history of cancer and have been exposed to various carcinogens in their work as a firefighter? Okay what about human males that are Greek and have a family history of cancer and have been exposed to various carcinogens in their work as a firefighter but have an extremely balanced and healthy diet? I could go on and on but let me land the plane here. Once we get nuanced we get a weird result…Eventually, you get a reference class with a sample size of one—me. And that leads to absurd results: a probability of either 0% or 100%. Clearly, something’s gone wrong.
Why is that a problem? If you’re sample size is one, and the probability of any X being true given its frequency in a sample size is equal to that frequency, then the only options for the probability of X being true is either 0 or 1 (0% or 100%). But that is a completely counter intuitive result! The more data you have, the closer you should get to the probability, not further away! In short, here’s the catch: the more you refine your reference class to include relevant information, the less data you have—and the more fragile your probability estimate becomes.
Here is what ends up happening, if you are too generalized with your reference class (in this case it was just “humans”) the less meaningful the probability is. The more nuanced and detailed you get, the further away you get from the actual probability!
Let me show you how this relates to the resurrection now.
Now apply this to Jesus. You start with the broad reference class:
All humans → no resurrections
Then refine:Humans named Jesus
Born ~7BC–2AD, died ~30–36AD
Crucified under Pontius Pilate
Had followers who later claimed to see him alive
Eventually, you’re down to one individual: Jesus of Nazareth. And if your reference class contains one case, your frequentist probability becomes either 0% or 100%—which is not rational.
Counter-Examples
Yet another issue with this line of reasoning is that it just falls prey to way too many counter examples. Ill give two, the first one being spicy, the second not being as spicy.
First example: Abiogenesis
Take abiogenesis: the origin of life from non-life. It has never been observed, never repeated, and the statistical frequency is… 0.
But would Paulogia say that means it didn’t happen? Of course not. Because other background data justifies it. And yet, when it comes to the resurrection, he pretends statistical frequency is all that matters.
Do we have any observed instances of abiogenesis? Have we been able to replicate it? The answer is no. Note: I am not arguing against abiogenesis here. I am simply showing how this logic when applied to other things we believe in produces results that are clearly not true.
If this was indeed the way to assess priors, then no amount of evidence for any abiogenetic model would ever be enough to say that life originated on earth at some point.
Another example: The Spring
Let’s rewind to whenever the first spring was ever invented. I don’t know when that was, so let’s just pretend it happened in the year 1900. It is the year 1900, and I come up to you and say:
“Look! I just invented this thing. I will call it a spring. But here’s an interesting question for you…What do you think the probability of the spring decompressing is if I compress it, and then let go? This has never been done before”
Are you feeling the issue here? The answer, given this method, is zero in this instance, but that is very clearly not the probability. There is something else going on that is informing us about what the prior probability actually is then right?
Different Types of Probability
There are other reasons to reject the frequentist metric, but I want to move on. Let’s explore what exactly is going on here and what the mistake is. Put simply, for both of the examples, there is a very simple answer to this.
Statistical probability is NOT the only type of probability!
While we could get into a lot of nuance there, let me just keep things simple by pointing out three different kinds and explain how they play into all this.
The three are physical probability, statistical probability, and inductive (or logical) probability. Here is a table summarizing the different types.
Physical probability is a matter of the extent to which at some event at an earlier time predetermines an event at a later time. In other words, it is a measurement of the extent some conditions predetermine an event to happen. The spring example is reliant on this!
Statistical probability is, to quote Swinburne, “a property of a class of things and is a measure of the proportion of things in the class that have some other property”. This is the kind of probability used to try and argue for a low prior for the resurrection of Jesus.
Inductive probability concerns the question “how much more probable is this proposition given this piece of information” (2004, p. 16). This is the type of reasoning we use all the time. We use it in science, history, crime, law, etc.
So what kind of probability do we need when evaluating something like the resurrection?
Answer: Inductive probability. The kind we use when asking:
“Given this background information and this testimony, how likely is it that this happened?”
All of this is extremely important because it all entails that our background knowledge can actually inform us on the prior probability of any hypothesis in spite of any statistical frequency!
That’s why the resurrection can be assessed probabilistically—even if its statistical frequency is 0.
The question isn’t:
“How often do resurrections occur?”
It’s:
“Given this testimony and background knowledge, how likely is it that one occurred here?”
And that’s a fundamentally Bayesian question.
Why The Prior Is Not All That Low For The Resurrection
So far, we’ve granted an extremely skeptical starting point. We said, “Fine — 1 in 1,000,000. Let’s run the numbers anyway.” And even then, the posterior climbed to nearly 88%. Then we looked at the arguments for the low priors that skeptics give and showed where they fail. Now we can dig into reasons why the priors for the resurrection may not be as astronomically low as the skeptic may think.
1. P(Miracles | Theism) is Not Low
If God exists — a being with power, knowledge, and purpose — then miracles are not inherently improbable.
They may be rare, but rare ≠ unlikely given the right conditions.
In fact, under theism, we’d expect:
That God would act in history
That He would intervene for axiologically significant reasons
That He might use miracles to communicate or validate truth
So when someone says “Miracles don’t happen,” we should ask:
“Given what? Atheism or theism?”
Because:
This matters — a lot. If you already believe in God (or are agnostic), then miracle claims aren’t starting at zero. To be clear, I am not saying one needs to presuppose God’s existence either. I am merely saying that if you are a Theist, or even an Agnostic, then we have a reason to think the priors are not infinitesimally small.
They’re plausible within the theistic framework.
2. P(Incarnation | Theism) is Also Not Low
Now we go deeper. I wish I had more space to unpack this all…but for now this will suffice.
Not only is a miracle plausible under theism — the incarnation and resurrection are especially so.
Let’s consider the logic:
If God exists and is perfectly good
And He wants to enter into relationship with human beings
And He wants to provide redemption, healing, and moral transformation…
Then the incarnation — God becoming man — fits beautifully.
And more than that: a vindicating miracle like the resurrection makes sense as part of this cosmic drama.
And this is where my Cosmic Story Theodicy and axiological structure enters:
If God wants a redemptive story
And that story involves suffering, death, and the defeat of evil
Then the resurrection of Christ functions as the narrative climax of that arc
This isn’t just “God did a cool thing once.” It’s the turning point of a cosmic narrative.
So under theism + axiological purpose, we find:
Because if God becomes incarnate to save the world, validating His mission through conquest of death is exactly what we’d expect.
AGAIN to be clear, I am being quick here for sake of brevity. I am writing a (currently 3 volume) book series on all this, where I cover all of this in extensive detail. If enough people want it, I will do a write up on these sorts of arguments. For now I highly recommend reading Dr. Sijuwade’s work “The Necessity of an Incarnate Prophet”
3. Modern-Day Miracles Further Support This
Someone might say:
“Sure, maybe that’s how it would go if God exists. But do we see this kind of thing happening?”
The answer is: yes.
As Craig Keener has documented in detail, there are thousands of modern miracle claims worldwide. They’re not all equally strong. But the sheer volume and pattern — many with corroboration — point toward something real. On top of that, I, alongside my friend Caleb Jackson, have done a lot of work on modern day miracles.
And this bolsters the prior:
The resurrection is not utterly unlike anything else ever claimed
It fits within a broader pattern of divine action that continues today
This raises the plausibility that something like this happened at the start of Christianity.
Therefore the prior for the resurrection is not just some arbitrary number plucked from thin air. It depends on your broader worldview.
Here’s how it stacks up:
Under naturalism, the prior is extremely low
Under theism, the prior is moderate to high
Under theism + incarnation + moral purpose, the prior is very high
We granted the lowest prior just to show how much weight the evidence could bear.
But the more you take theology and metaphysical background into account, the less that burden is needed.
In short: the resurrection is not only defensible in spite of the prior — it becomes expected once the right framework is in place.
Testing the Resurrection With More Accurate Priors
We’ve now seen two things:
Even under radically low priors, the resurrection hypothesis dramatically outperforms its competitors.
That low prior wasn’t warranted to begin with if we’re working under a theistic framework.
So let’s take the next step and run the numbers again — but this time with more accurate priors that reflect the wider metaphysical context.
Step 1: Assign a Neutral Prior for Theism
Let’s assume, for the sake of argument, that we’re agnostic between atheism and theism. That is:
Step 2: Assign Prior Probabilities Conditional on Theism
Next, we ask: if God exists, what is the probability that He would become incarnate in human history?
While I personally think the Theism entails (or at the very least makes extremely likely) an incarnation…. I will assign a low value for dramatic effect:
Now: if God does become incarnate, what’s the probability that He would validate that incarnation through resurrection — given our background knowledge…defeating death and inaugurating redemption?
This is much higher, say:
Now we chain the conditionals..
Step 3: Chain the Priors to Get P(Resurrection)
We’re going to calculate:
Insert the numbers:
So now we have a 4.5% prior instead of 0.0001%.
That’s a 450× increase in the starting plausibility of the resurrection even with me extending the skeptic an olive branch!
Step 4: Rerun the Cumulative Bayesian Case
Let’s plug this prior into the very same cumulative framework we ran earlier — just swap in 0.045 at the start instead of 0.000001.
Since all the likelihood ratios (from E₁, E₂, and E₃) remain the same, you’ll see that the final posterior soars.
In fact, even after just one or two lines of evidence, you’ll already have very strong confirmation.
Low priors are not a death sentence. They can be defeated with strong evidence.
But the prior itself was never that low to begin with if we’re working in a theistic worldview:
If God exists, miracles are expected
If God is good, incarnation is likely
If God incarnates, resurrection is probable
Cumulative priors matter. And when they’re built on solid philosophical foundations, they make the resurrection highly plausible before we even begin counting evidence.
Bonus: Paulogia’s Talking Dragon Analogy (And Why It Backfires)
If you’ve read this far and are thinking-
“Than, you have no way of knowing this is what’s going on in Paul’s head based a on a simple tweet!”
Here’s the thing. I am a mind reader
In all seriousness I am making inferences — sure. But that’s not a flaw. That’s literally what historical reasoning does: we infer intentions, reliability, and plausibility based on contextualized patterns. And that’s exactly what Paulogia claims to do when arguing against the resurrection. So it would be inconsistent to fault that very method here.
And I’m not guessing. I’m tracking a pattern.
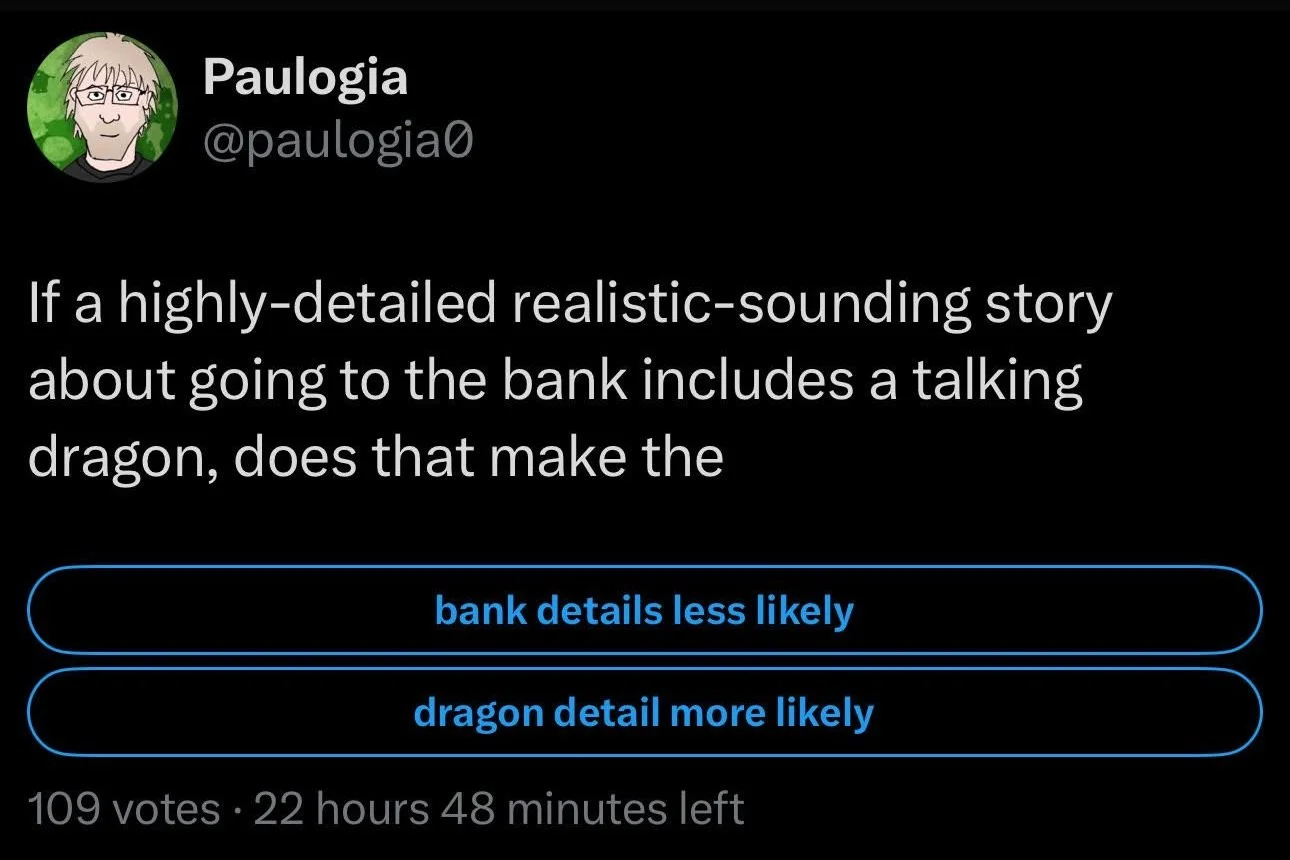
Take this tweet, posted a few days after the original thread we analyzed:
Let’s pause here.
This is a parody of the maximal data case. He’s implying that detailed realism in one part of a story does not justify believing the miraculous part.
But if that’s the point, then Paulogia has — again — misunderstood the argument.
No one is saying:
“Because some details are accurate, everything must be.”
That would be a clear non sequitur.
Instead, the maximal data case says:
“The data we find in the Gospels and Acts is more expected on the HRM relative to any of the skeptical models of the Gospels and Acts”
And that in turn raises the likelihood of certain kinds of testimony — which then get evaluated using Bayesian criteria, not naïve credulity.
But wait — there’s more.
In this video at the 25 minute mark (and other places) Paulogia says:
“When an apologist says maximal case for the resurrection, what they mean is that secondary literature has affirmed for them that it’s okay to simply believe the non-mundane claims in the primary literature because they’re adjacent to mundane claims… which is just [that] with extra steps.”
That’s not only a mischaracterization — it perfectly confirms what I’ve been arguing all along.
He thinks the problem is the non-mundanity of the claims.
He thinks apologists are just smuggling in miracle claims by riding on the back of mundane ones.
He sees no epistemic weight in testimony for the miraculous — because his prior is too low to budge.
Which brings us back to where this all started.
This isn’t just a disagreement about data. It’s a breakdown in how probability works when testimony concerns something extraordinary.
If Paulogia thinks historical realism in the Gospels doesn’t raise the probability that the authors are honestly reporting what they believed they saw, then his skepticism isn’t just against miracles — it’s against inference itself. Taken to its logical end, this is an outright denial of math!
And that’s the real problem this isn’t just a philosophical misstep. It’s mathematical malpractice.
Mistake #1: Misunderstanding the Maximal Case
No maximal data argument says:
“If some parts of the story are realistic, then everything must be true.”
That would be an obvious fallacy.
What we actually argue is:
The cumulative historical realism — undesigned coincidences, name frequency congruence, local knowledge, etc. — significantly increases the probability that the source is aiming to report experienced events, not invent them.
And if we assume the Gospels and Acts are broadly reliable reportage (the HRM), then the likelihood of the resurrection testimony occurring under that model is far higher than if the accounts are late, literary, or legendary.
In other words, realism in mundane details raises the prior for sincere testimony — and that affects how we evaluate miraculous claims.
But instead of engaging this line of reasoning, Paulogia sidesteps it by conflating credibility of testimony with credibility of the event itself, treating it all as one undifferentiated “belief leap.”
Mistake #2: Letting the Prior Corrupt the Model
Worse, there’s a probabilistic error lurking underneath.
Paulogia (and many others) let their low prior on miracles influence how they model the Gospels:
They assume the Gospels can’t be historically reliable,
Because that would make a miracle more likely,
And miracles can’t be likely.
That’s circular reasoning. It's the Bayesian version of sawing off the branch you’re sitting on.
The proper move is to first model the Gospels independently of the resurrection — assess whether they are likely sources of historical reportage. If they are, then that becomes part of your k (background knowledge) when calculating the likelihood of a resurrection report.
But if your miracle priors automatically veto the historical model, then your Bayesian machinery is rigged from the start.
Let’s be explicit. If:
P(E∣HRes+k)≫P(E∣HAlt+k)
Then the evidence favors the resurrection hypothesis — regardless of your prior — unless you’re assigning a prior of literal zero, which has it’s own whole host of issues. Nonetheless, I don’t think Paulogia would endorse a 0 prior either!
Mistake #3: Misidentifying What’s Actually Moving the Needle
This clip from Paulogia (around the 25-minute mark) confirms what’s happening under the surface:
“When an apologist says ‘maximal case for the resurrection,’ what they mean is that secondary literature has affirmed for them that it’s okay to simply believe the non-mundane claims in the primary literature because they’re adjacent to mundane claims… which is just [that] with extra steps.”
This is exactly what we’ve been saying he gets wrong.
He assumes that the maximal data approach tries to smuggle in belief in the resurrection by riding the coattails of mundane details.
But what it actually does is show that the probability of the testimony increases under the resurrection hypothesis — which is a valid evidential move under Bayesian inference.
The mistake, then, is not merely philosophical. It’s not just about what he finds plausible. It’s about failing to consistently apply the very logic of evidential reasoning that he claims to use.
The Real Problem
This isn’t a debate about a few ancient documents.
This is a debate about the structure of rational belief revision.
If you think realism in a document can’t raise the likelihood that its authors believed what they claimed — then you’re rejecting historical reasoning.
If you think testimony can’t update priors — then you’re rejecting probability theory.
And if you think miracle priors can veto modeling decisions — then you’re not doing inference. You are just foot stomping.
The Talking Dragon Analogy Doesn’t Work
So lets just take on his silly tweet. Paulogia’s “talking dragon” tweet is meant to parody maximal data reasoning. The structure of the analogy is:
“If a highly-detailed realistic-sounding story about going to the bank includes a talking dragon, does that make the dragon more likely?”
Intuitively, the answer seems like “no” — and that’s what the skeptic wants you to conclude:
That mundane detail doesn’t boost the plausibility of extraordinary claims.
But there’s a big problem: This analogy collapses under formal analysis.
The Analogy Confuses Events with Testimony About Events
Suppose we have two hypotheses:
H₁: The story is fabricated or fictional (e.g., someone made it up).
H₂: The story is sincere testimony — the author is reporting what they believed happened.
Now let E = a document containing multiple true mundane details + one extraordinary claim (e.g., a talking dragon).
So what do we ask in Bayesian terms?
We’re not asking whether:
We’re asking whether:
And that can go up — dramatically — when the details are:
Unexpected
Accurate
Confirmed independently
Known only by someone present
Distributed unintentionally (undesigned)
And more
This is precisely how we reason about historical testimony, journalism, and even courtroom eyewitnesses.
In Formal Terms: Likelihood Ratio Clarifies the Issue
Let’s define:
HT= the author is sincerely testifying
HF = the author is fabricating or inventing
E = the collection of realistic and historically congruent details in the story
Now we ask: Which hypothesis makes the evidence more expected?
That is:
LR= Likelihood Ratio
If the document includes dozens of accurate, hard-to-fake, contextual, or interlocking details, then:
P( E | HT) >> P( E | HF)
Which means:
LR≫1
This raises the probability that the author is testifying, not inventing. And that matters when the testimony includes extraordinary claims. I am not saying this means the dragon was real. All this entails is what I am saying, which is, again, merely that the author is testifying honestly. This is the same thing as when we argue that the details in the gospels and acts increase the probability of HRM over any skeptical model.
A Counter-Example
If you still don’t see the issue here is a counter-example. Imagine someone says:
“I was assaulted on 5th Street at 11:42pm. The car was blue, license plate NY2934, and a man in a red jacket grabbed me near the bus stop outside Emilio’s Deli. When he attacked me, he spoke as if he had 10 different voices coming out of him! Like a legion of demons!”
Now suppose:
All the mundane details check out.
The deli exists, the timestamp matches CCTV, and a man in a red jacket is seen there.
Would that not make the core testimony more credible?
We’re not saying the red jacket proves the demon voice. We’re saying that accuracy in detail increases the probability that the author is reporting, not inventing. The explanation for demon part of her testimony could be that she is mistaken, or could be that it was a demon! This example is merely pointing out the the presence of something “non-mundane” in testimony does not render the testimony less reliable.
Let’s now apply this to Jesus vs. the dragon.
TL:DR?
Congrats Paul. Mundane details don’t prove miracles. But when they multiply and cohere, they make sincere testimony more likely. And if the resurrection is being sincerely reported, that’s a massive update. A talking dragon in a bank story isn’t that. Jesus in history might be.
Conclusion
We’ve now walked through a structure of reasoning that most people—skeptics and believers alike—have never seen applied this rigorously to the resurrection. Most people are used to a "minimal facts” style approach where we take a few vague data points and try to argue from there. This is not like that. This article was only a small taste of the argument from a larger scale. There is a lot we did not cover, including the objections you are probably thinking about right now! Covering all that would just entail writing a whole book (which for those interested….I am indeed working on a book series that is at least 3 entries long thus far related to all this).
Nonetheless, this is a structured argument that follows a lot of nuance. We began by assuming a deeply skeptical prior—just a one-in-a-million chance that Jesus rose from the dead. And we didn’t try to argue that number up. We left it there. Then, piece by piece, we evaluated how much more expected the historical evidence is under the resurrection hypothesis than under any of its competitors. And we watched the scales move—not arbitrarily, but mathematically.
That’s the power of Bayesian reasoning: it doesn’t ask for blind leaps. It just asks you to trace what would be more expected if one hypothesis were true rather than another. And as we’ve seen, even if your initial assumptions are stacked against the resurrection, the cumulative force of the evidence forces a reevaluation.
This isn’t about proving the resurrection with certainty.
It’s about showing that dismissing it as “too improbable” is no longer intellectually honest—at least not without dealing seriously with the data.
If you're still skeptical, that’s okay. But now the burden is on you.
You can’t simply wave your hand and say, “Miracles don’t happen.”
You have to offer a better model. One that makes the evidence we have more expected than the resurrection hypothesis does. Not just “possible.” Not just “maybe.” But more probable—step by step.
And that’s the question that still hasn’t been answered by critics like Paulogia:
Given this data, and given this model, what alternative explains it better?
Until that question is answered with equivalent rigor, the maximal data case for the resurrection stands—not as wishful thinking, but as an inference to the best explanation.
Editors Note- This is an academic-level version of the more pop level response I wrote.
If you want a more condensed and simpler read, please consider reading that version instead.
Sources & Recommended Reading
Keener, Craig S. Christobiography: Memory, History, and the Reliability of the Gospels. Eerdmans, 2019.
Eddy, Paul R., and Gregory A. Boyd. The Jesus Legend: A Case for the Historical Reliability of the Synoptic Jesus Tradition. Baker Academic, 2007.
Bock, Darrell L. Studying the Historical Jesus: A Guide to Sources and Methods. Baker Academic, 2002.
Hume, David. An Enquiry Concerning Human Understanding. Edited by Tom L. Beauchamp, Oxford University Press, 2000.
McEleney, Neil J. "The Principles of Historiography." Theological Studies, vol. 28, no. 1, 1967, pp. 1–20.
Swinburne, Richard (2004). The existence of God. New York: Oxford University Press.
Swinburne, Richard (2003). The Resurrection of God Incarnate. Oxford, GB: Clarendon Press.
Swinburne, Richard, The Christian God ( Oxford , 1994; online edn, Oxford Academic, 1 Nov. 2003)
Sijuwade, Joshua (2023). The Necessity of an Incarnate Prophet. Religions 14 (8):1-45.
Earman, John (2000). Hume's abject failure: the argument against miracles. New York: Oxford University Press.
https://plato.stanford.edu/entries/probability-interpret/
“The Formal Epistemology of Miracles” By Tim McGrew - https://www.youtube.com/watch?v=GH11Ur8cjwM
David J.C. MacKay Information Theory, Inference, and Learning Algorithms
E. T. Jaynes Probability Theory: The Logic of Science
https://plato.stanford.edu/entries/bayes-theorem/#:~:text=Another%20useful%20form%20of%20Bayes,)%2FP(~H).
https://plato.stanford.edu/entries/epistemology-bayesian/
TIMOTHY MCGREW AND LYDIA MCGREW The Argument from Miracles: A Cumulative Case for the Resurrection of Jesus of Nazareth
Lydia McGrew - Hidden In Plain View: Undesigned Coincidences in the Gospels and Acts
Lydia McGrew - The Eye of the Beholder: The Gospel of John as Historical Reportage
Lydia McGrew - Testimonies to the Truth: Why You Can Trust the Gospels
Lydia McGrew - The Mirror or the Mask: Liberating the Gospels from Literary Devices
Tim and Lydia McGrew - Internalism and Epistemology: The Architecture of Reason (Routledge Studies in Contemporary Philosophy)